导读:
控释系统(CRSs)是生物活性化合物(BCs)定点递送的重要平台,但受非均一性、结构不稳定等问题制约。近期,有研究人员采用电流体动力学(EHD)工艺,将胶体(cCNC)与交联(xCNC)两种形式的纤维素纳米晶体分别与海藻酸盐(ALG)复合,成功制备出形状均一、pH敏感的水凝胶微球(HMs),并通过模拟胃肠道环境验证了其对亲/疏水生物活性化合物的可控释放性能,为解决控释系统非均一性与结构不稳定问题提供了新方案。相关研究以“Cellulose nanocrystal-based hydrogel microspheres prepared via electrohydrodynamic processes for controlled release of bioactive compounds”为题目,发表在期刊《Carbohydrate Polymers》上。
本文要点:
1、本研究采用电流体动力学(EHD)工艺,将两种形态的纤维素纳米晶体(CNC:胶体态cCNC、交联态xCNC)与海藻酸盐(ALG)复合,制备形状均一的水凝胶微球(HMs),用作pH敏感型BCs控释载体。
2、以疏水和亲水染料为模型BCs负载于HMs,其球形因子≤0.05,尺寸随电压变化,范围为 ∼1200 μm(电压关闭)至300 μm(电压打开)。
3、在模拟胃(pH 2.4)和小肠(pH 8.2)环境中,采用Korsmeyer-Peppas模型分析释放机制,释放指数(n)表明,染料通过非费克扩散(0.43≤n≤0.85)和Case-II转运(n≥0.85)实现pH依赖性释放。
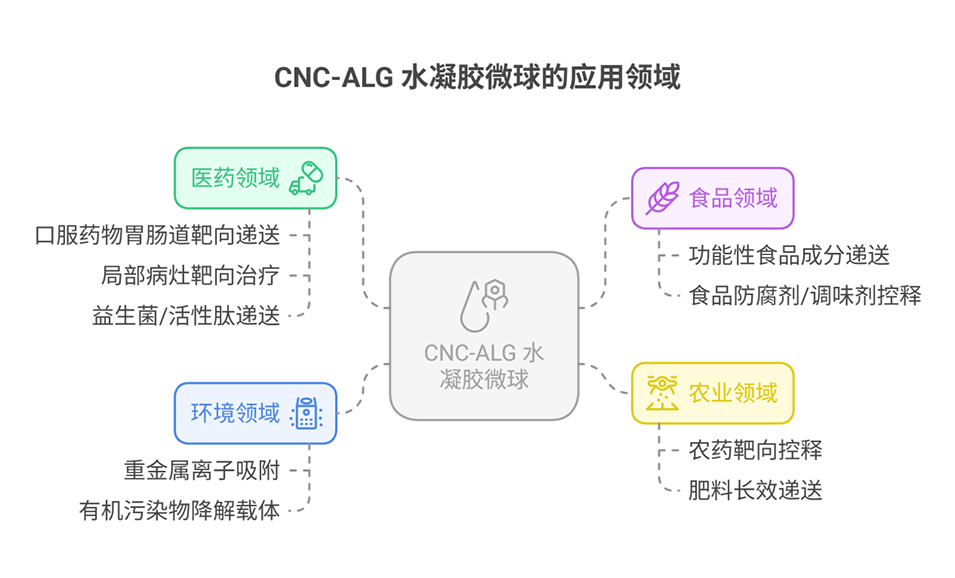
电流体动力学(Electrohydrodynamic, EHD)工艺是一种利用电场力调控流体行为,实现微纳米级材料制备的先进技术,核心是通过电场与流体力学作用的耦合,将流体(如聚合物溶液、溶胶等)转化为形态、尺寸可控的微球、纤维或薄膜等结构,在生物医药、材料科学等领域应用广泛,尤其适用于生物活性化合物(BCs)载体(如水凝胶微球)的精准制备。
其基本原理是:将待处理的流体(如研究中的ALG/CNC复合溶液)装入带针头的注射器,通过注射泵控制流速将流体推向针头尖端;同时在针头与接地的收集装置(如含氯化钙的收集浴)间施加高压电场,使针头尖端的流体因电荷积累发生形变(形成“泰勒锥”),随后在电场力、表面张力、粘性力等共同作用下,流体被拉伸、破碎为微小液滴或连续纤维;最终液滴在收集浴中固化(如研究中ALG与钙离子交联),形成目标微结构(如水凝胶微球)。
该工艺的关键优势在于:
1、精准调控产物形状与尺寸:通过调节电压(如研究中0kV→10kV使微球尺寸从1200μm缩至300μm)、流速(如2.5ml/h更易形成球形微球)、流体粘度等参数,可实现产物尺寸(纳米级至微米级)、形状(球形、纤维状等)的精准控制;
2、生物相容性好:过程温和(无需高温、强化学试剂),能有效保留BCs(如药物、益生菌)的活性,适合生物医药载体制备;
3、制备效率高:操作简单且可连续生产,易于规模化应用,在控释系统、组织工程支架、功能材料等领域具有重要价值。
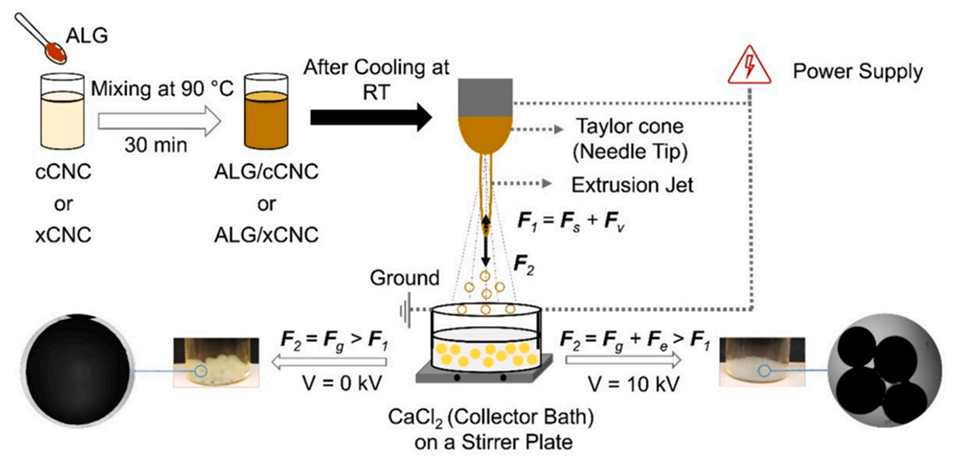
图1 电流体动力学(EHD)工艺制备微球的分步流程及微球形成过程中涉及的作用力示意图。其中,F1 为表面张力(Fs)与粘性力(Fv)之和,F2 为重力(Fg)与电场力(Fe)之和。
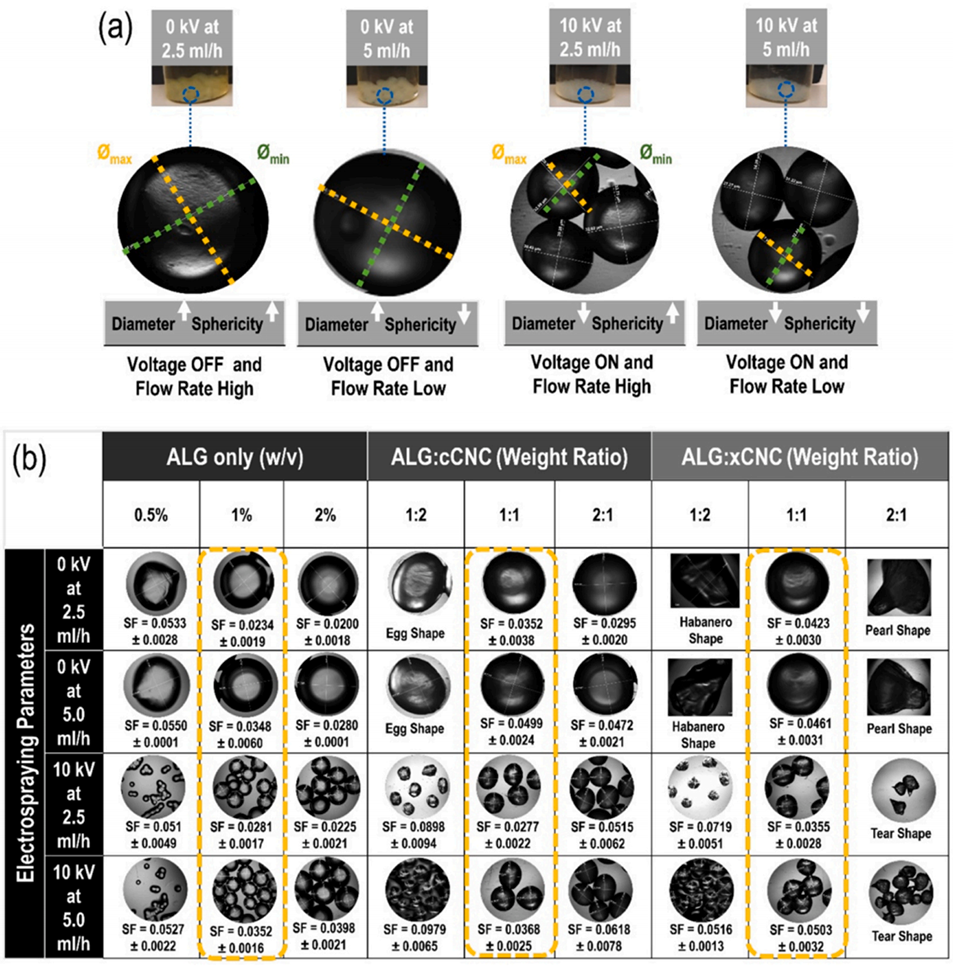
图 2 工艺方案优化:(a)工艺参数对微球形貌的影响;(b)不同组成体系下电流体动力学工艺制备微球的效果。
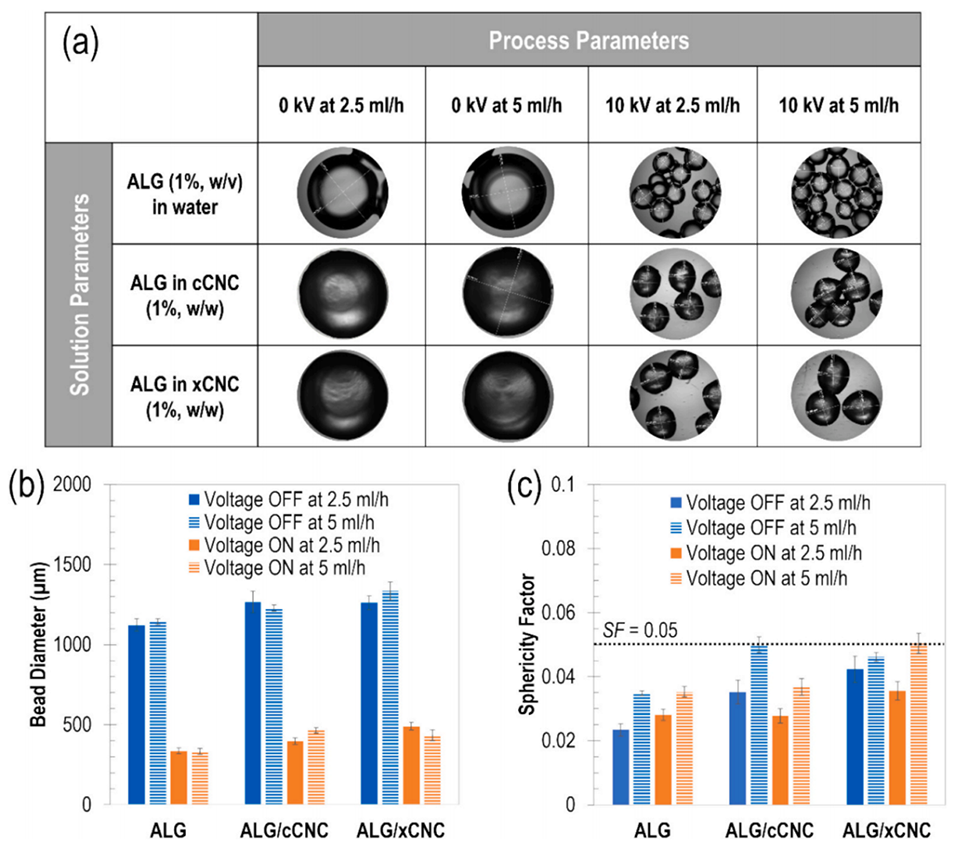
图 3 所制备水凝胶微球在测试条件下的理想特性确定:(a)电动力学参数(组成与工艺);(b)尺寸;(c)形状。
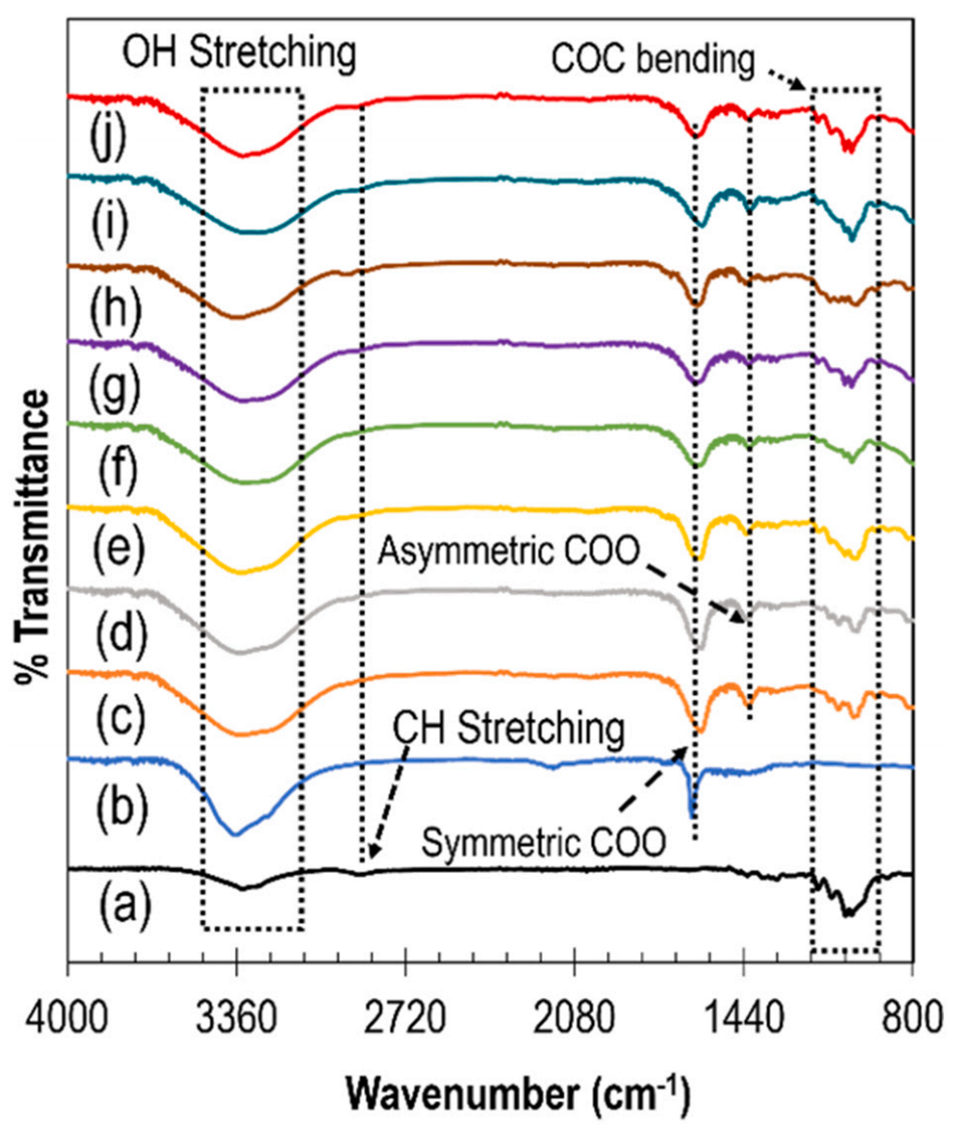
图 4 用于表征对照组及其复合体系(负载与未负载染料)化学键特征的傅里叶变换红外(FTIR)光谱图。具体包括:(a)对照纤维素纳米晶体(CNC);(b)对照海藻酸盐(ALG);(c)负载柠檬黄的 ALG;(d)负载三联吡啶氯化钌(II)(rubpy)的 ALG;(e)ALG/cCNC 对照体系;(f)负载柠檬黄的 ALG/cCNC;(g)负载 rubpy 的 ALG/cCNC;(h)ALG/xCNC 对照体系;(i)负载柠檬黄的 ALG/xCNC;(j)负载 rubpy 的 ALG/xCNC。其中,柠檬黄为亲水性染料,rubpy 为疏水性染料。
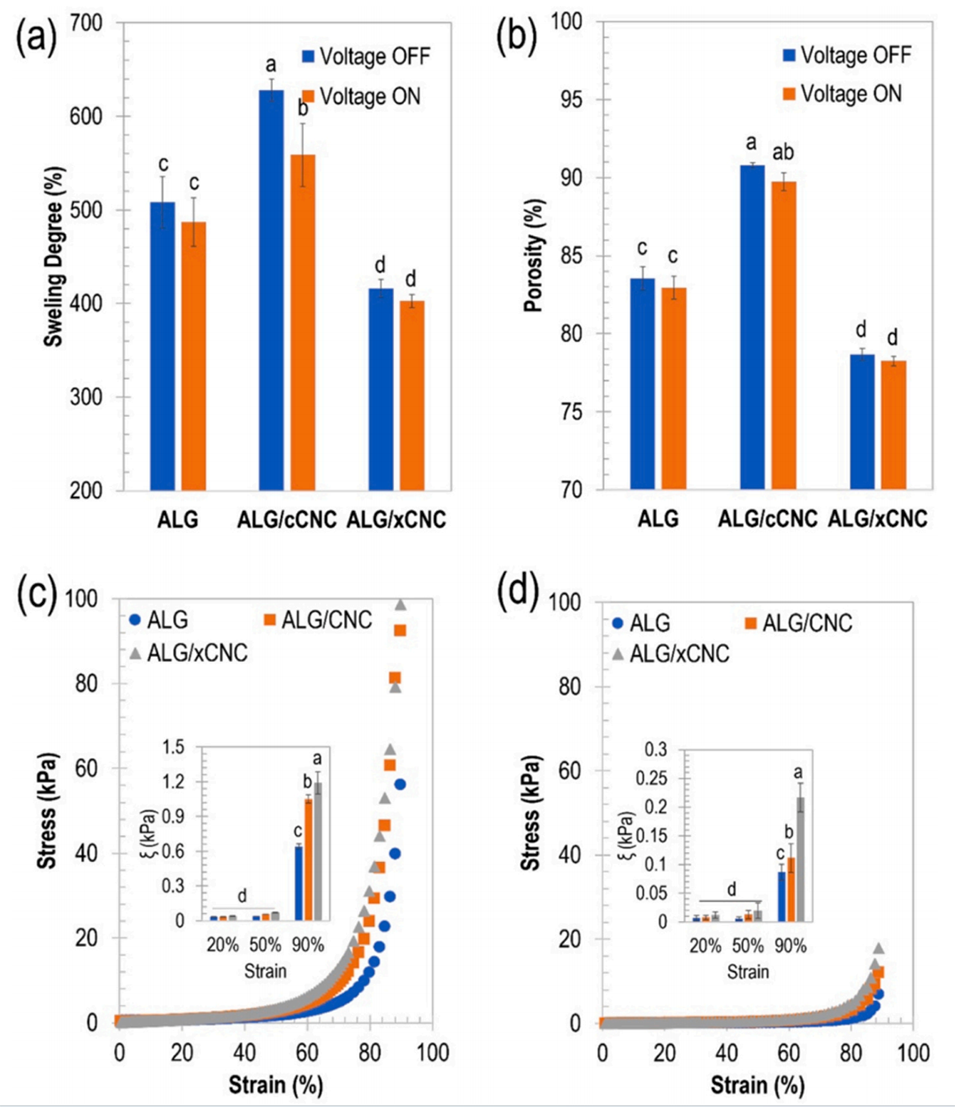
图 5 微球性能评估。(a)溶胀度,(b)孔隙率,(c- d)压缩试验结果(c 为电压关闭状态,d 为电压开启状态)。
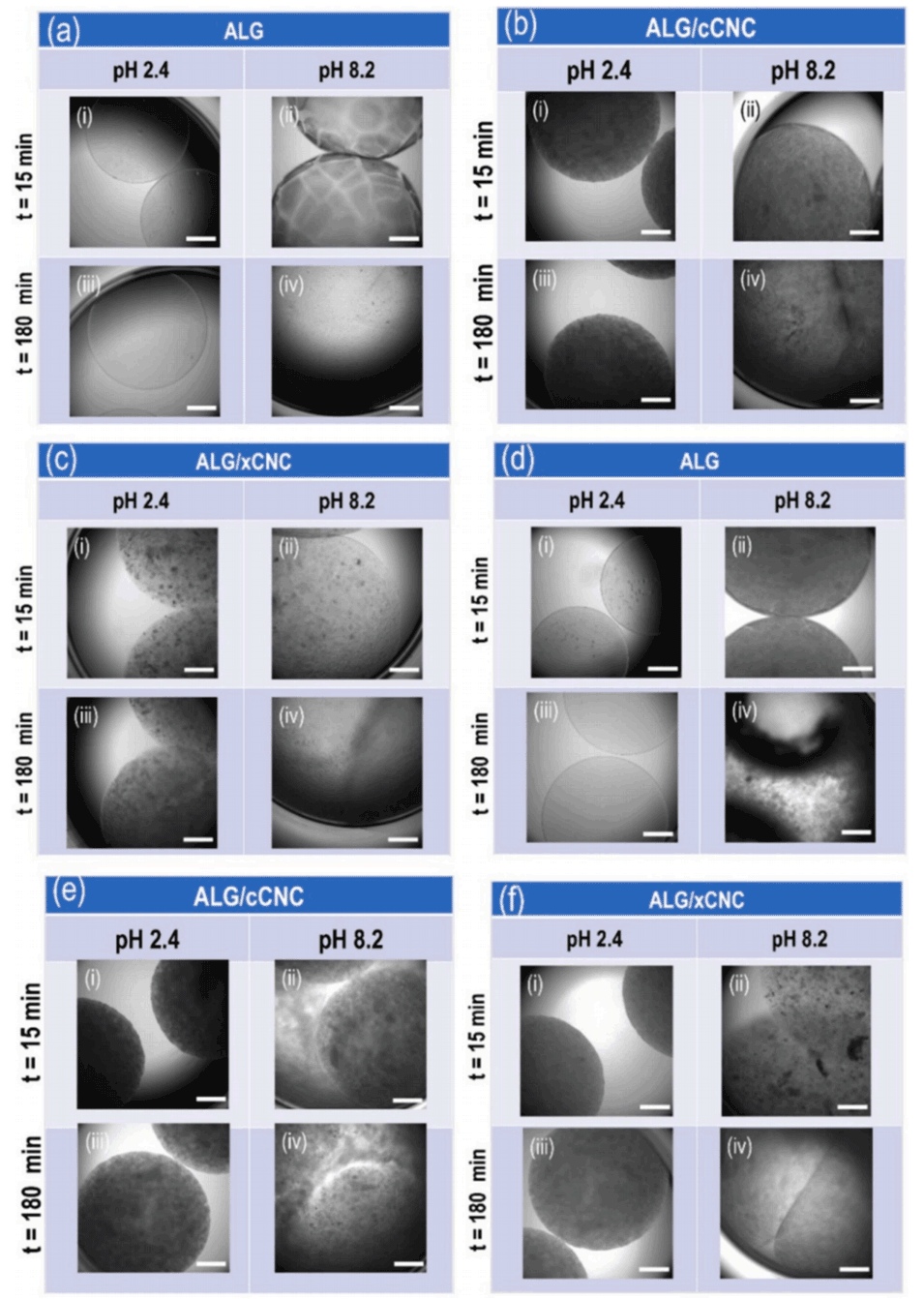
图 6 不同 pH 条件对负载染料微球影响的显微照片。(a- c)负载柠檬黄的微球,(d- f)负载 rubpy 的微球。
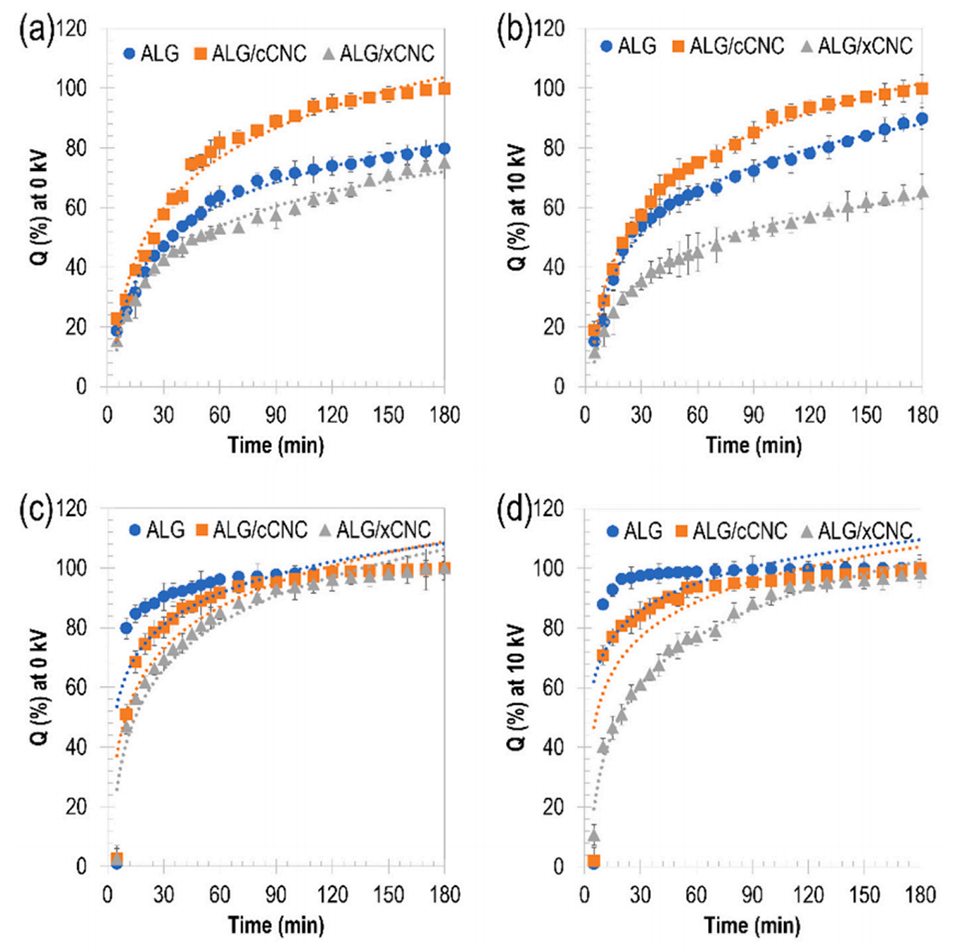
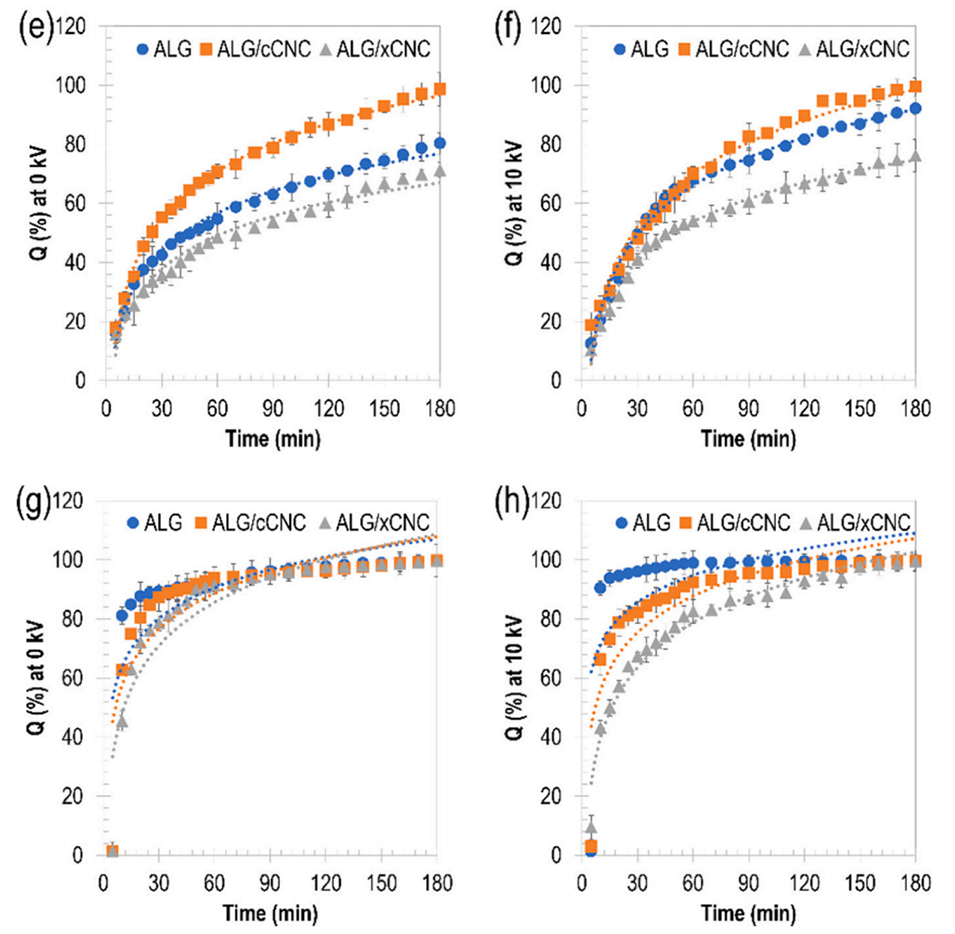
图 7 不同组成及电压条件下制备的微球中染料的累积释放曲线。(a- d)柠檬黄的释放曲线[(a)pH 2.4、0 kV;(b)pH 2.4、10 kV;(c)pH 8.2、0 kV;(d)pH 8.2、10 kV];(e- h)rubpy 的释放曲线[(e)pH 2.4、0 kV;(f)pH 2.4、10 kV;(g)pH 8.2、0 kV;(h)pH 8.2、10 kV]。每条曲线上的虚线为拟合线,代表 Korsmeyer-Peppas 模型。
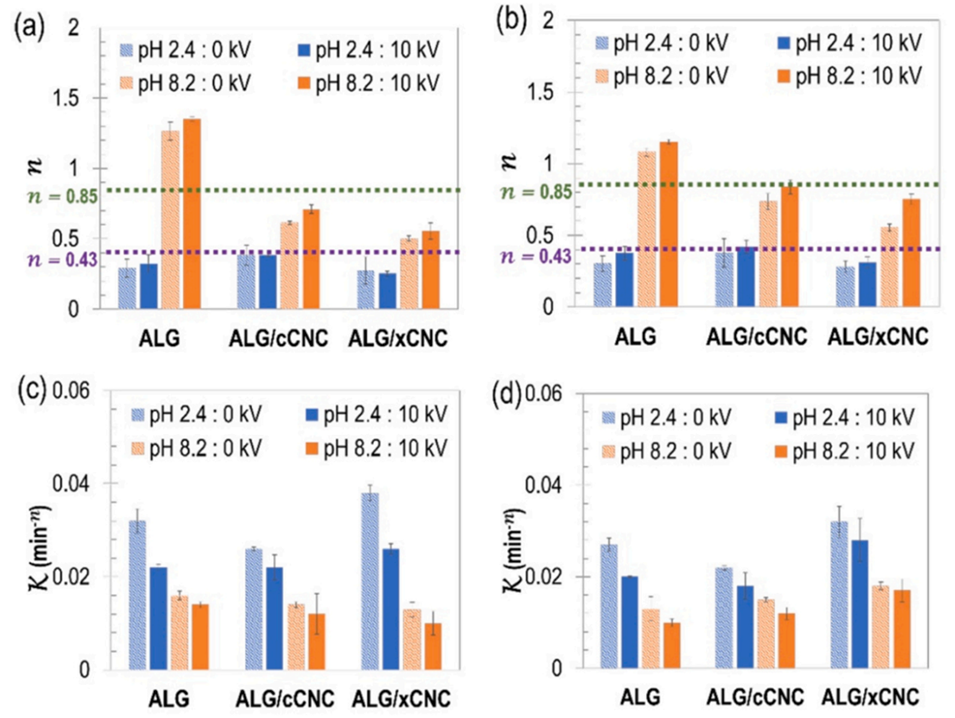
图 8 基于 Korsmeyer-Peppas 模型参数的释放动力学机制分析。(a, b)释放指数[(a)柠檬黄,(b)rubpy];(c, d)动力学速率常数[(c)柠檬黄,(d)rubpy]。
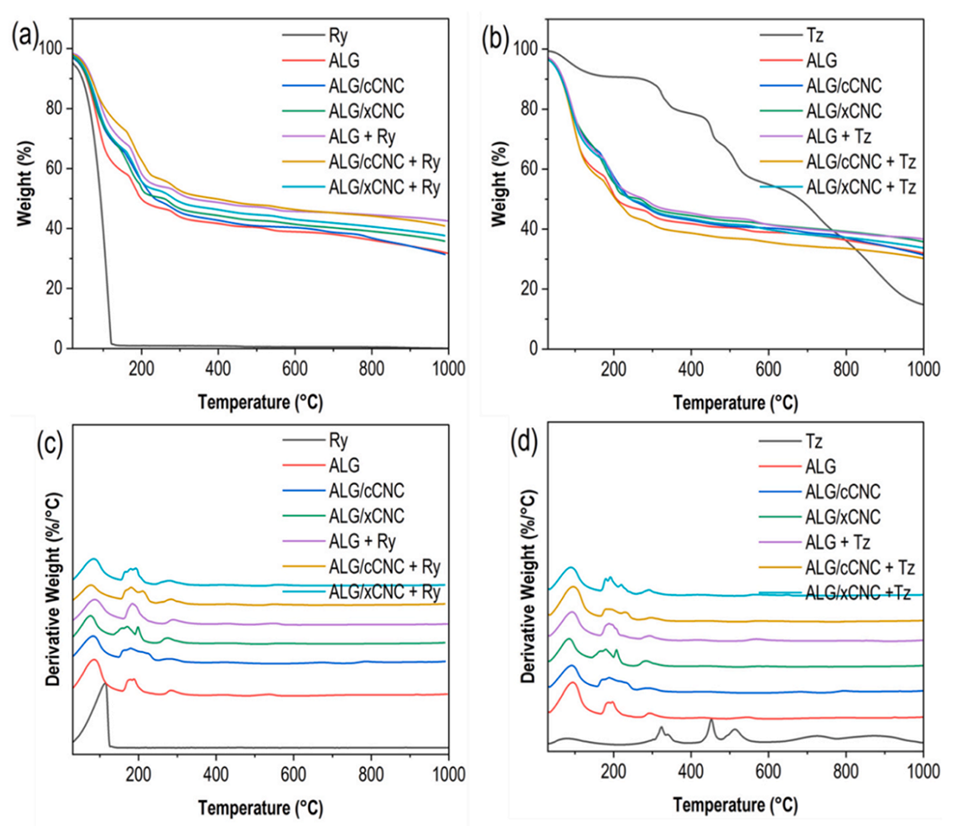
图 9 水凝胶微球(HMs)的热稳定性分析。(a- b)热重分析(TGA)曲线[(a)负载 rubpy(Ry)的微球,(b)负载柠檬黄(Tz)的微球];(c- d)对应的导数热重(DTG)曲线[(c)负载 Ry 的微球,(d)负载 Tz 的微球]。
论文链接:https://doi.org/10.1016/j.carbpol.2025.123355
(本文仅供参考学习及传递微流控研究成果,版权归原作者所有,如侵犯权益,请联系删除)